💻Character Level Named Entity Recognition using RNNs

Introduction

We train a recurrent neural network (an LSTM) from scratch to classify characters that belong to different entities. Specifically, we leverage named entity recognition (NER) to classify delimiter characters in log data. Delimiters are characters that act as separators, similar to punctuation marks in natural language.

We do not use any pre-trained models. We train our NER model from scratch.

The code associated with this post can be found in this GitHub repository (which can also be run in Google Colab). The code is written in TensorFlow, but it should be relatively easy to translate it to other frameworks (e.g. PyTorch).

Purpose of training network

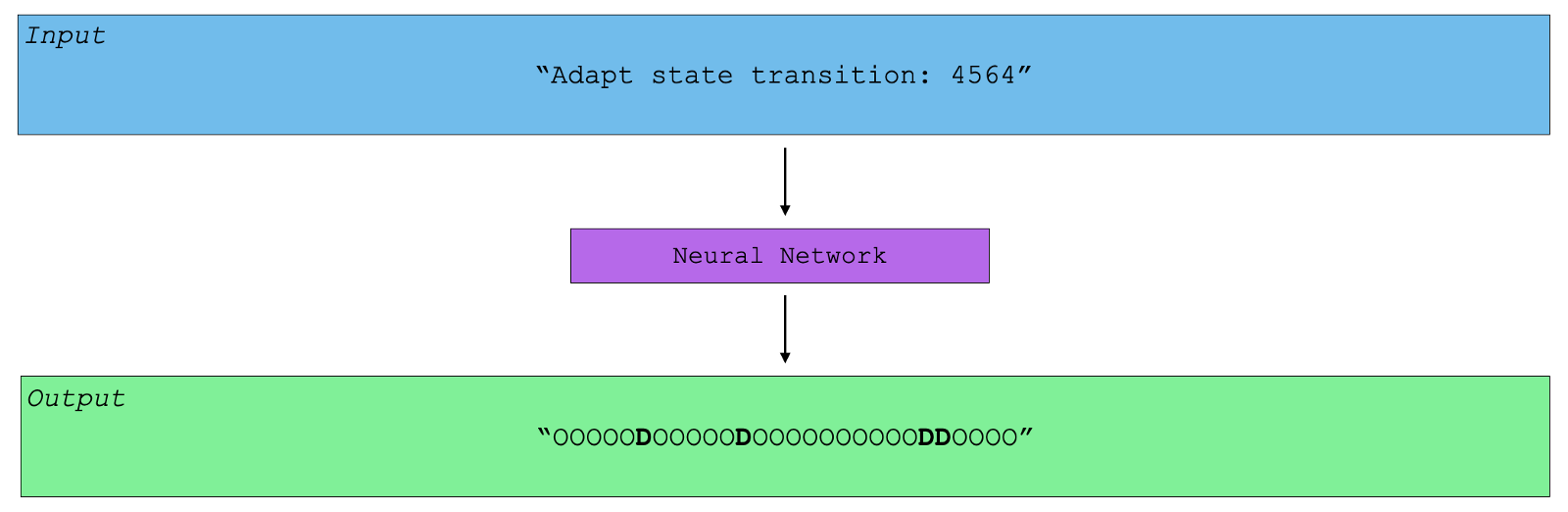
Binary classification of characters in a log message. Given an input message, we want to classify each character, with either (1) “O” (the constant class) or (2) “D” (the delimiter class). Below, we visualize the output of our neural network. Given a log message, our neural network is able to identify the delimiter characters, and subsequently label them with “D”.

Training Data

Each training data point contains a sequence of characters (a log message) with its corresponding labels. Each character can either belong to the ‘O’ or ‘D’ class. Below, we print one of the entires in our dataset.

# example training entry
[['A','d','a','p','t','e','r',' ','s','t','a','t','e',...,'u','n','t','i','l'],
 ['O','O','O','O','O','O','O','D','O','O','O','O','O',...,'O','O','O','O','O']]

Data preparation

We need to transform our characters into numbers, as we are going to use tensors. Thus, we create vocabularies for (1) the characters in our training data and (2) the labels associated with every character. Next, to be able to manipulate these vocabularies, we create (1) a character-to-index dictionary, (2) an index-to-char dictionary, (3) a label-to-index dictionary, and (4) an index-to-label dictionary.

# create character/id and label/id mapping
char2idx = {u:i+1 for i, u in enumerate(vocab)}
label2idx = {u:i+1 for i, u in enumerate(labels)}

# print(char2idx)
# {' ': 1, '0': 2, '1': 3, '2': 4, ...}

Data objects for training and testing

We need to create data objects for the train/test/validate steps. Each of the train/test/validate samples is transformed in tensor format. Below, we print an example of an input-target pair.

# print example input
# tf.Tensor(
# [[25 28 39 24 12 37 35 38 24  1 42 24 36  1 33 34 36  1  4  5  6 10  1 22
#  31 20 42  1 27 28 23 24  1 20 32  1  3  4  5  6  1 26 28 39 24 33  1 28
#  36]], shape=(1, 49), dtype=int32)

# print example target
# tf.Tensor(
# [[2 2 2 2 1 2 2 2 2 1 2 2 2 1 2 2 2 1 2 2 2 2 1 2 2 2 2 1 2 2 2 2 1 2 2 1
#  2 2 2 2 1 2 2 2 2 2 1 2 2]], shape=(1, 49), dtype=int32)

Building and training our LSTM model

We train a simple LSTM model. We use a batch size of 128, an embedding dimension of 256, and 1024 RNN units.

# batch size
BATCH_SIZE = 128

# The embedding dimension
embedding_dim = 256

# Number of RNN units
rnn_units = 1024

# Number of labels
label_size = len(labels)

# build LSTM model
def build_model(vocab_size,label_size, embedding_dim, rnn_units, batch_size):
      model = tf.keras.Sequential([
          tf.keras.layers.Embedding(vocab_size, embedding_dim,
                            batch_input_shape=[batch_size, None],mask_zero=True),
          tf.keras.layers.LSTM(rnn_units,
                      return_sequences=True,
                      stateful=True,
                      recurrent_initializer='glorot_uniform'),
          tf.keras.layers.Dense(label_size)
          ])
      return model

We train the model for 20 epochs.

Epoch 1/20
2559/2559 [==============================] - 68s 25ms/step - loss: 0.0065 - sparse_categorical_accuracy: 0.9973 - val_loss: 1.2535e-06 - val_sparse_categorical_accuracy: 1.0000
Epoch 2/20
2559/2559 [==============================] - 64s 25ms/step - loss: 5.6644e-07 - sparse_categorical_accuracy: 1.0000 - val_loss: 2.2188e-07 - val_sparse_categorical_accuracy: 1.0000
...
Epoch 20/20
2559/2559 [==============================] - 65s 25ms/step - loss: 5.6644e-07 - sparse_categorical_accuracy: 1.0000 - val_loss: 2.2188e-07 - val_sparse_categorical_accuracy: 1.0000

Evaluation

We print below our confusion matrix and classification report.

              precision    recall  f1-score   support

         1.0       1.00      1.00      1.00        10
         2.0       1.00      1.00      1.00        37

    accuracy                           1.00        47
   macro avg       1.00      1.00      1.00        47
weighted avg       1.00      1.00      1.00        47

References

The GitHub repository associated with this post.

💻Character Level Named Entity Recognition using RNNs.